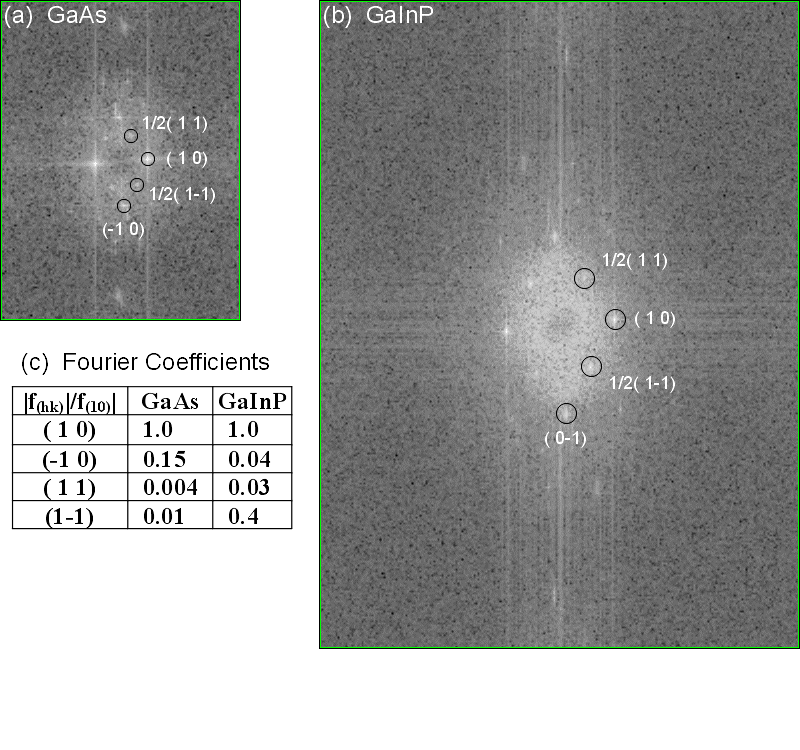
Fig. 6: Fourier Space images of the GaInP (a) and GaAs (b) regions of Fig. 4. Diffraction spots are labeled according to their 2-D Miller Indices, where [ 1 0] is in the [ 0 0 1] direction and [ 0 1] is in the [ 1 -1 0] direction. Both images show the expected ( 1 0) and ( 0 1) "diffraction" spots, due to the lines of atoms along the [ 0 1] or [ 1-1 0] and [ 1 0] or [ 0 0 1] directions, respectively. The GaInP image shows relatively intense 1/2( 1-1) and 1/2( 1 1) spots. The GaAs image also shows these spots, however, they are 10 and 40 times less intense, respectively, and insignificant. In the GaInP image the 1/2( 1-1) spot is about 10 times more intense than the 1/2( 1 1) peak. The 1/2( 1-1) peak is associated with a tendency of In to align in every second line of atoms running in the [ 1 1] or [ 1-1 2] direction, while the 1/2( 1 1) spot is associated with a tendency of In to align in every second line of atoms running in the [-1 1] or [-1 1 2] directions. The fact that the former peak is much more intense indicates that the form of ordering associated with this spot is much more prevalent. This can be directly observed in the direct-space image of Fig. 4(b) by looking along the [ 1-1 2] and [-1 1 2] directions and noting that there are more lines of In atoms observed in the [ 1-1 2] direction.

[Click on figure to enlarge]



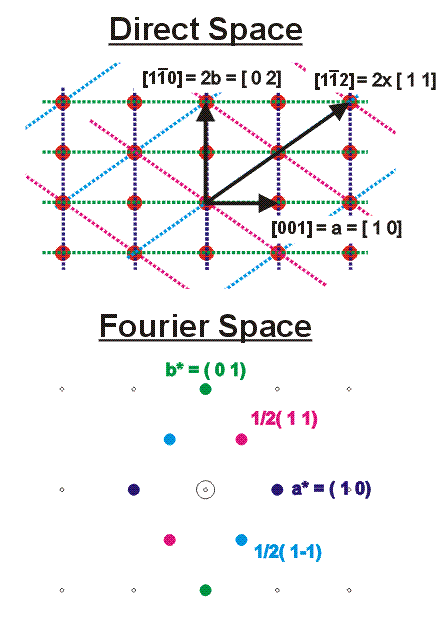Fig. 6+: Diagram of Direct and Fourier Space Representations. The direct space diagram shows the usual GaAs(110) 2-D rectangular lattice. To show the connection between this 2-D lattice to its Fourier representation, two dimensional indices are introduced, such that, [001] or a is [ 1 0], and [ 1-1 0] or 2 x b is 2 x [ 0 1]. With this two dimensional representation, the meaning of the indexed diffraction spots becomes clearer (hopefully). The diffraction spots are labeled in the usual way, i.e. with the Miller Indices of the set of lines (lines in 2-D, not planes) of atoms that would give rise to these spots through diffraction. For example, using reciprocal lattice vectors a* and b*, a spot at ha*+kb* from the origin, is represented by the Miller indices (h k ) which represents the periodicity in the direct space image associated with the set of Miller "lines". That is, the ( 1 0) spot shown in blue is associated with periodicity shown by the blue dotted lines, and the 1/2( 1 1) magenta spot is associated with periodicity shown by the magenta dotted lines, etc.. Note, the 1/2( 1 1) family of lines are every second line of the ( 1 1) family. Thus the 1/2( 1 1) spot represents the tendency of In to be in alternate ( 1 1) Miller "lines" (the lines that are directed in the [ 1-1] or [-1 1 2] direction) and the 1/2( 1-1) spot represents the tendency of In be in alternate ( 1 -1) Miller "lines" ( the lines that are directed in the [ 1 1] or the [ 1-1 2] direction). Note in 3-D the [hkl] direction is normal to the (hkl) planes, whereas in 2-D the [hk] direction is normal to the (hk) lines. Of course, that this is for a cubic (square) lattice, but our 2-D lattice is rectangular, so for us the [hk] direction is "nearly" normal to the (hk) lines.